5. Boundary Layer¶
One of the most important things in a fluid mechanics simulation is how the boundary layer is taken into account in the simulation.
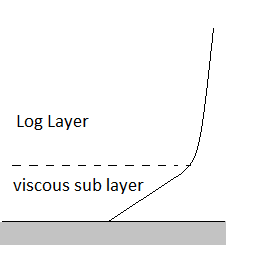
In order to have a well re-transcribed boundary layer, we have to ensure that there are enough points in the boundary layer.And, since the solution obtained depends on the location of the first cell, we have to make sure that the center of the first cell is well-located meaning that it has the adequate y+. For the Spinupstrat Case with K-Omega SST :
- if there are no wall functions : the center of the first cell has to be located in the sub-viscuous layer
- \(y+\in[1; 30]\)
- if there are wall functions : the center of the first cell has to be located in the log layer
- \(y+\in[30; 100]\)
The initial mesh available on the various tutorials was a uniform one, meaning that the discretization of the x, y and z axis are uniform (no gradient). The size of each cell on the z axis was 2.5 cm. We displayed the value of y+ in the center of the first cell.
- We consider the solid rotation so we can display the velocity in a section of the cylinder (as showed on the figure upward) :
- \(U = \frac{\omega R}{2}\)
- We can then estimate the value of u_* using the following approximation :
- \(u_* \simeq \frac{U}{10}\)
- Finally, y+ is defined as :
- \(y = y_+\frac{\nu}{u_*}\)
For a simulation using water as the fluid, we found a value of approximately y+ = 800 for the center of the first cell (uniform mesh). This value is way too high which means that all the gradients are poorly estimated/calculated. To correct the problem, we thought of improving the basic original mesh by refining it near the bottom wall. We did not directly change the complete mesh of one of the available simulations. We thought it better to create a whole new simulation that would be more adapted to deal with meshrelated issues. A whole new simulation called spin-up strat piece was created.