2. Tutorials¶
2.1. The parameters of the tutorials¶
The tutorials and their results depend on the parameters defined in certain files. Below are described these files.
2.1.1. 0_init¶
- Requires : dimensions, internal field (set value in domain), boundaryfield (set boundary conditions)
- Contains values :
- alphat = turbulent viscosity
- P = pressure
- p_rgh = dynamic pressure
- rhok = density
- U = velocity
2.1.2. Constant¶
- polymesh file : contains blockMeshDict, blockMeshDict_orig, make_blockMeshDict.py. These are programs to change the mesh
- g : defines gravity field
- MRFproperties : set platform rotation speed
- transportproperties : set values laminar viscosity, Prandtl number, turbulent Prandtl number
- turbulence properties : sets simulation type :
- Laminar (direct simulation)
- RAS (Reynolds Average Simulation)
- LES (Large Eddy Simulation)
2.1.3. System¶
- controldict : sets input parameter, essential for database creation (timesteps, simulation period/length)
- decomposeParDict : modifies number of processors used, and how they are used
- funkySetFieldsDict : sets density gradient
- fvSchemes : numerical schemes (implicite, explicite)
- fvSolution : equation solver,tolerances and algorythms control
- topoSetDict : Operates on cellSets/faceSets/pointSets through a dictionary (by default system/topoSetDict). The results are stored in constant/polyMesh/sets
2.1.4. .sh files¶
- clean.sh : This command is used to remove the initial files created from any previous simulations like the time directories and the polymesh content in “Constant”.
- init_simul.sh : This command generates the mesh from the “blockmeshDict” file and copies the “0_init” information into coriofoam.
- init_parallel.sh : This command decomposes a case to be run in parallel, it uses the file “decomposeParDict”.
- launch_sequencial.sh : This command is used to launch the simulation on the computer and the output is sent to “log.txt”.
- lauch_parallel_local.sh : This command defines the number of cores with the dict file and sets the output to “log.txt”.
- lauch_parallel_cluster.sh : This command launches a parallel simulation and should be used with the cluster. The simulation job is named with the time and date. It sets the output to “log.txt”.
2.1.5. other files¶
- template.oar (This is were simulation outputs usually go when they are not redirected to “log.txt”)
- plotcontourux.py (plots the ux contour in center plane with python)
- empty_for_paraview (This is used to view the simulation results with paraview)
2.2. Tutorial gravitational_instability_norot¶
The time 0 of this case has a density stratification which is higher at the top than at the bottom. The platform contains a fluid whiwh is similar to honey and rotates at a speed of 0.2 rad/s. Thus the evolution of the fluid is determined by the influence of gravity and of the coriolis force. This simulation uses 4 processors.

2.3. Spinup case simulation¶
The time 0 of this case has a density stratification which is lower at the top than at the bottom. The platform contains a fluid whiwh is similar to honey (nu = 0.01, Pr = 7) and begins to rotate at a speed of 0.2 rad/s. This simulation uses 16 processors.
The fluid with the higher density latches very quickly onto the edges of the platform. The fluid doe snot become homogeneous with time, there is still a separation in the density of the fluid. After a long time the higher density stays closer to the edges even if there is a strong diffusion.

2.4. Spinup stratificated komega case¶
Initially this case also has a density stratification which is lower at the top than at the bottom. The platform contains a fluid whiwh is similar to water (nu = 10-6, Pr = 7) and begins to rotate at a speed of 0.2 rad/s. But a k-omega turbulence model has been implemented. This simulation uses 16 processors.
The results are similar to the spinup case with honey but they take a lot longer to reach the final state, in fact we did not have the time to reach it.
2.5. Interpretation and Validation of the Solver and the K-Omega Model¶
One of the important question we had to answer was whether the K-Omega model is useful or not. In order to do so we had to run the spin-up strat simulations on water, with and without the K-Omega model, on water. We then plotted the velocity evolution for the two cases :
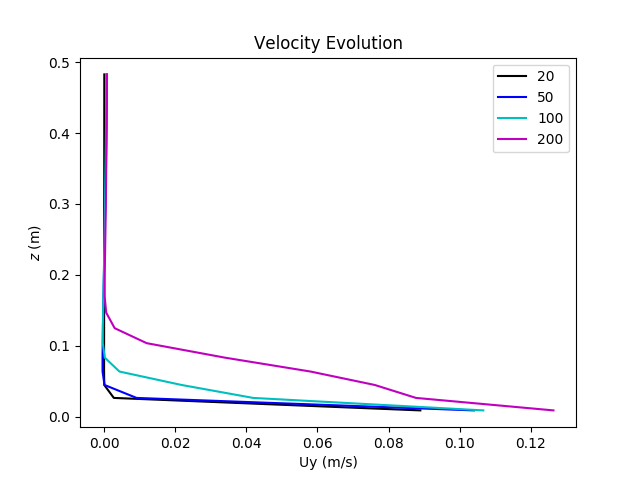
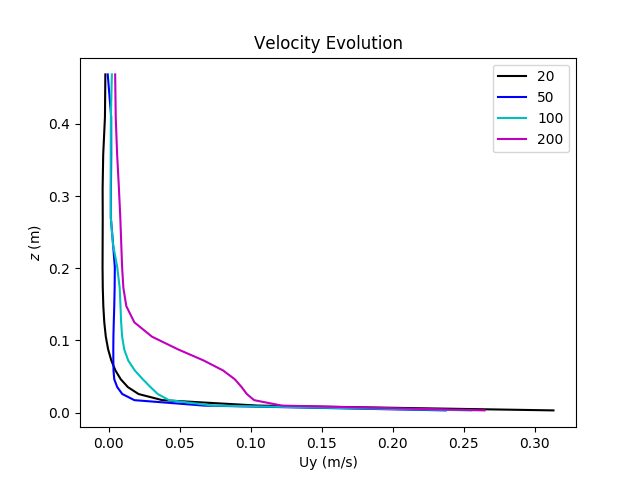
Concerning the physics behind problem, at the beginning (between time 0 and 100), there is no turbulence therefore there is only the rotation of the molecules. Since there is only the rotation of the molecules, the only mechanism at work is the molecular viscosity, which explains that there are very important velocity gradients at the beginning of the experience. Then, turbulence appears and is diffused in the flow. But since the turbulent viscosity is 1000 times larger than molecular viscosity, the gradients can no longer be enormous, so we witness a diminution of the velocity gradients when time passes. On the graph located on the left, the effect of turbulence diffusion on the velocity profile is obvious (time 200), whereas on the right the profile obtained is not very precise (time 200). Moreover the profiles on the left seem smoother whereas the profiles on the right seem to be discontinuous, they are not very well rendered. The velocity profile displayed with K-Omega seems to be more accurate, so the K-Omega model is necessary.
2.6. Spinup stratificated piece of cake case¶
For calculation time reasons, a new simulation was created. The idea was to reduce the calculus domain to a small “piece of cake” to accelerate the calculations. The initialisation of this case is the same as the SpinupStrat K-Omega case.
2.7. Center cylinder¶
The initial condition at t = 0 of this new tutorial is the following; the platform is rotating in permanent regime, it means that the case of solid rotation is valid. In the center of the platform, there is a cylinder of fluid with a higher density than the fluid outside of it. At time t = 0, the fictive border between the two fluid with different densities disappears.
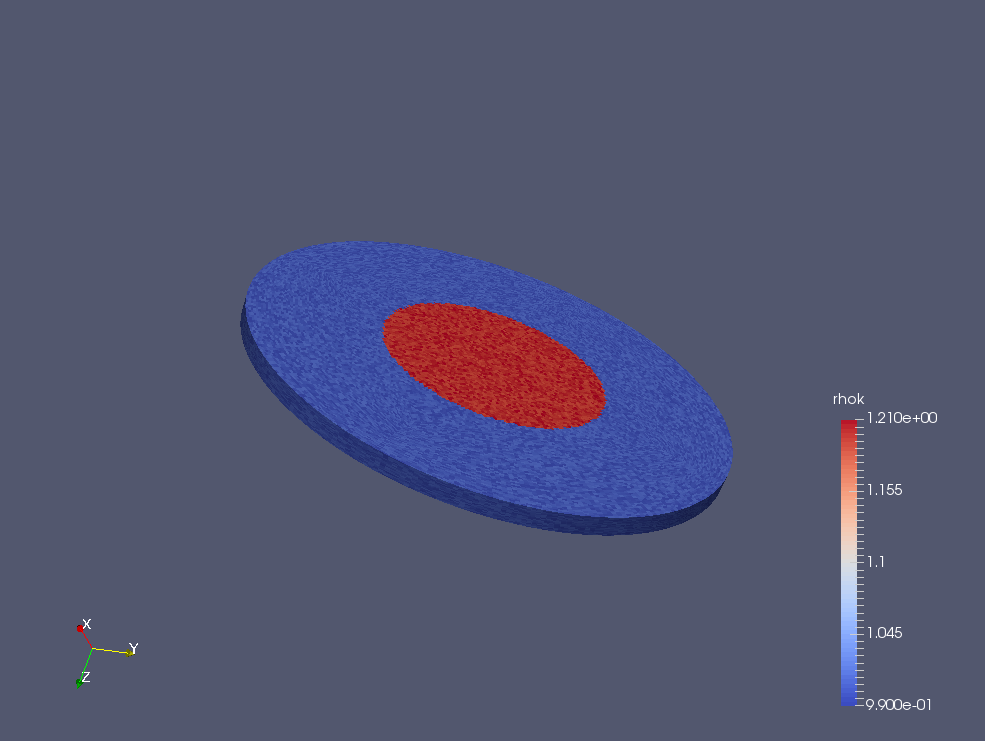
Thanks to this tutorial, we would like to bring out the Coriolis effect. At time t=0, we are in solid rotation to avoid a quick mix between the two phases. The expected effect is the following; the center cylinder will collapse because of gravity, and the dense fluid will go to the edges because of the inertial force. But we hope that the trajectory of a particle of fluid will be deviated (it means that it will not follow a radius) on the right, to bring out the Coriolis effect.
The work of initialization must be made in the file named “funkysetFields”, located on the folder “system”.
- Conditions on density
We define the density field (rhok) with the following expression on C++ language:
{
variables
(
"center_cylinder_radius=3;"
);
field rhok;
expression "(sqrt(pow(pos().x,2) + pow(pos().y,2))) < center_cylinder_radius ? 1.2 + 0.01 * 2 * (rand() - 0.5) : 1. + 0.01 * 2 * (rand() - 0.5)";
}
It means that for each point located in the 3 meters wide cylinder (value which can be modified in the script), the density is imposed to 1.2 and the density is equal to 1.0 everywhere else. In the expression, we introduce a part of randomness with the rand() function. It is useful to have a model which is more realistic than a “perfect numerical simulation”. Without this precaution, it would be difficult to model something with a realistic evolution. Thanks to the non-uniformity of the field, some imperfections appear and those imperfections will enable the code to evolve correctly.
- Conditions on Velocity
The velocity is given by: U = rω for a solid rotation:
{
variables
(
"w=0.2;" //rotation speed
);
field U;
expression "vector(w * sqrt(pow(pos().x,2) + pow(pos().y,2)) *
(pos().x/sqrt(pow(pos().x,2) + pow(pos().y,2))) , w *
sqrt(pow(pos().x,2) + pow(pos().y,2)) * (pos().y/sqrt(pow(pos().x,2) + pow(pos().y,2))),0)";
}
- Conditions on Pressure
Because of the solid rotation, the pressure field is not uniform. There was a difficulty since the numerical model does not represent exactly what is happening in the reality. On the real platform, the surface of fluid is a free surface and during an experiment, the free surface is determined by the relation:
gradP = −ρg + ρrω2ur
After resolution, the mathematical expression of the free surface is:
\(z=z_0+\frac{\omega² r²}{2g}\)
The expression of the pressure is:
\(P=rho*g*(z - z_0)+\frac{\rho\omega² r²}{2}\)
The definition of the pressure field is specified in C++ language as fol- lows:
{
variables
(
"w=0.2;" //rotation speed
"z0=-2943;"
"g=9.81;"
"rho=1000;" //water
);
field p_rgh;
expression "rho * g * (pos().z - z0)+rho * ((pow(w,2) * pow(sqrt(pow(pos().x,2) + pow(pos().y,2)),2)/2))";
}
The definition of the pressure field might not be correct, because there were many problems with the pressure field. It has to be defined with one constant on a particular point. It means that the valeu of pressure has to be define on a chosen place of the platform. But imposing this value creats a special point which becomes a kind of anomaly for the simulation. Moreover, the definition of p and p-rgh are sometimes confusing, and it is difficult to know which field needs to be registerd. It exists also situations where the code requires adimensionnal values but it is also difficult to know when. Those problems made the tutorial unsucessful because we did not succeeded to launch a correct simulation.
A solution can be to impose the pressure field not only on a point, but on the complete surface (for example on the surface on the top) for each time step. It might give a more stable simulation. But there is still a problem with this proposal. As seen before, the pressure field depends on the density but it is not uniform on the top surface. For the first step, it is not difficult to define the pressure field with the condition on the radius but for the next step : the density field is unknown !
A lack of time did not enable us to go further for this tutorial, but we hope that those indications will be useful for others.
2.8. Post processing¶
Python codes :
- plot_crosssection.py : Plots the density of a section at a chosen time and plots the velocity on a section also at a certain time.
- plot_crosssection_profiles.py : Plots the velocity on the z axis from a point where the radius is equal to ‘ m at a chosen time.
- plot_evolution.py Thanks to this script we can visualize the evolution of the velocity profile. This can help us determine how close we are to the solid rotation.
- plot_bottom_boundary.py : This script helps vizualize the velocity value of the first points at the bottom of the tank. We can vizualize how the boundary layer is calculated and the errors due to bad mesh.